Calculus AB and Calculus BC
- 7 4 Slope Field Sap Calculus Solver
- 7 4 Slope Field Sap Calculus Formulas
- 7 4 Slope Field Sap Calculus Calculator
- 7 4 Slope Field Sap Calculus Equation
Slope fields show up on both the AP Calculus AB and BC tests. While at first this topic might seem daunting, the questions on the test are actually quite straightforward. Just keep one thing in mind: Go with the flow! A slope field shows the direction of flow for solutions to a differential equation. Need Calculus Math Help? The point P(7, −4) lies on the curve y = 4/(6 − x). If Q is the point (x, 4/(6 − x)), use your calculator to find the slope mPQ of the secant line PQ (correct to six decimal places) for the following values of x. SLOPE FIELDS - Differential Equations - Calculus AB and Calculus BC - is intended for students who are preparing to take either of the two Advanced Placement Examinations in Mathematics offered by the College Entrance Examination Board, and for their teachers - covers the topics listed there for both Calculus AB and Calculus BC. 7B Slope of Curve 4 Definition: The slope of a function, f, at a point x = (x, f(x)) is given by m = f '(x) = f '(x) is called the derivative of f with respect to x. Other names for f '(x): slope instantaneous rate of change speed velocity EX 2 Find the derivative of f(x) = 4x - 1. Slope Fields and Differential Equations Students should be able to: Draw a slope field at a specified number of points by hand. Sketch a solution that passes through a given point on a slope field. Match a slope field to its differential equation. Match a slope field to its solution.
CHAPTER 9 Differential Equations
B. SLOPE FIELDS
In this section we solve differential equations by obtaining a slope field or calculator picture that approximates the general solution. We call the graph of a solution of a d.e. a solution curve.

The slope field of a d.e. is based on the fact that the d.e. can be interpreted as a statement about the slopes of its solution curves.
EXAMPLE 1
7 4 Slope Field Sap Calculus Solver
The d.e. tells us that at any point (x, y) on a solution curve the slope of the curve is equal to its y-coordinate. Since the d.e. says that y is a function whose derivative is also y, we know that
y = ex
is a solution. In fact, y = Cex is a solution of the d.e. for every constant C, since y′ = Cex = y.
The d.e. y′ = y says that, at any point where y = 1, say (0, 1) or (1, 1) or (5, 1), the slope of the solution curve is 1; at any point where y = 3, say (0, 3), (ln 3,3), or (π, 3), the slope equals 3; and so on.
In Figure N9–1a we see some small line segments of slope 1 at several points where y = 1, and some segments of slope 3 at several points where y = 3. In Figure N9–1b we see the curve of y = ex with slope segments drawn in as follows:
FIGURE N9–1a
FIGURE N9–1b
Figure N9–1c is the slope field for the d.e. Slopes at many points are represented by small segments of the tangents at those points. The small segments approximate the solution curves. If we start at any point in the slope field and move so that the slope segments are always tangent to our motion, we will trace a solution curve. The slope field, as mentioned above, closely approximates the family of solutions.
FIGURE N9–1c
EXAMPLE 2
The slope field for the d.e. is shown in Figure N9–2.
(a) Carefully draw the solution curve that passes through the point (1, 0.5).
(b) Find the general solution for the equation.

FIGURE N9–2
SOLUTIONS:
(a) In Figure N9–2a we started at the point (1, 0.5), then moved from segment to segment drawing the curve to which these segments were tangent. The particular solution curve shown is the member of the family of solution curves
y = ln x + C
that goes through the point (1, 0.5).
FIGURE N9–2a
FIGURE N9–2b
(b) Since we already know that, if then we are assured of having found the correct general solution in (a).
In Figure N9–2b we have drawn several particular solution curves of the given d.e. Note that the vertical distance between any pair of curves is constant.
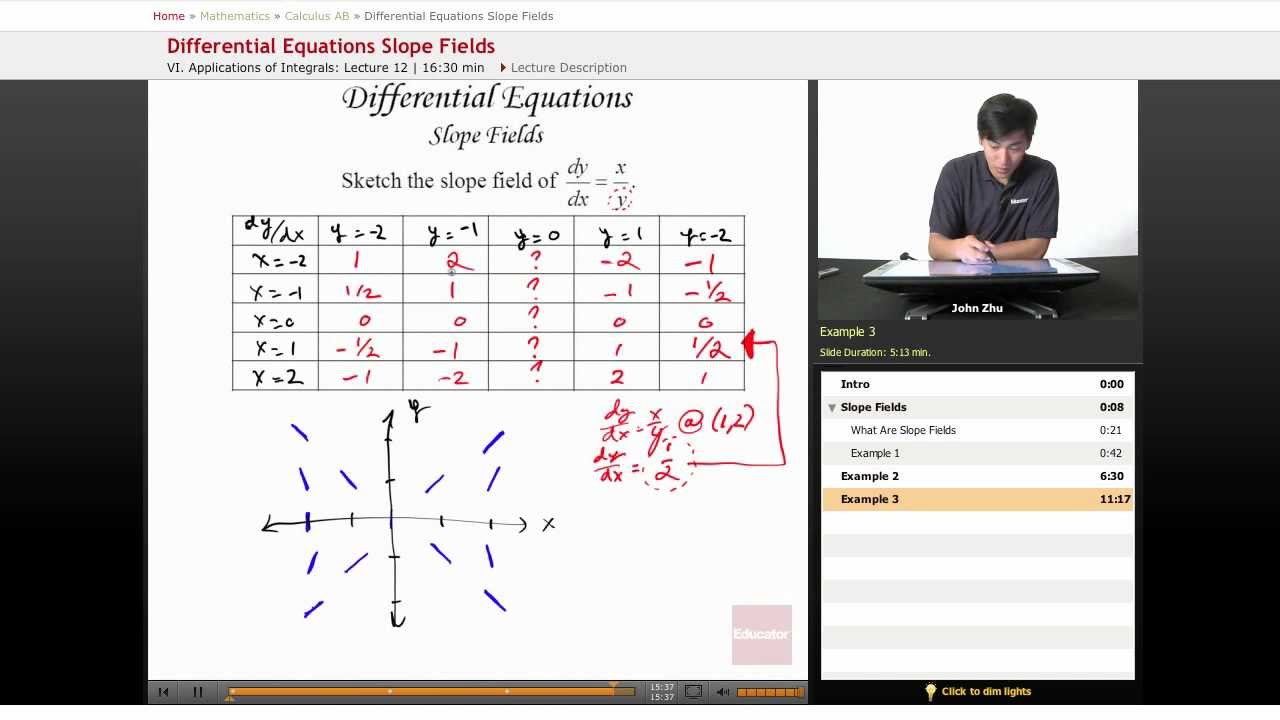
EXAMPLE 3
Match each slope field in Figure N9–3 with the proper d.e. from the following set. Find the general solution for each d.e. The particular solution that goes through (0,0) has been sketched in.
(A) y′ = cos x
(B)
(C)
(D)
FIGURE N9–3a
FIGURE N9–3b
FIGURE N9–3c
FIGURE N9–3d
7 4 Slope Field Sap Calculus Formulas
SOLUTIONS:
(A) goes with Figure N9–3c. The solution curves in the family y = sin x + C are quite obvious.
(B) goes with Figure N9–3a. The general solution is the family of parabolas y = x2 + C.
For (C) the slope field is shown in Figure N9–3b. The general solution is the family of cubics y = x3 − 3x + C.
7 4 Slope Field Sap Calculus Calculator
(D) goes with Figure N9–3d; the general solution is the family of lines y =

EXAMPLE 4
(a) Verify that relations of the form x2 + y2 = r2 are solutions of the d.e.
(b) Using the slope field in Figure N9–4 and your answer to (a), find the particular solution to the d.e. given in (a) that contains point (4, −3).
FIGURE N9–4
SOLUTIONS:
7 4 Slope Field Sap Calculus Equation
(a) By differentiating equation x2 + y2 = r2 implicitly, we get 2x + 2y from which which is the given d.e.
(b) x2 + y2 = r2 describes circles centered at the origin. For initial point (4,−3), (4)2 + (−3)2 = 25. So x2 + y2 = 25. However, this is not the particular solution.
A particular solution must be differentiable on an interval containing the initial point. This circle is not differentiable at (−5,0) and (5,0). (The d.e. shows undefined when y = 0, and the slope field shows vertical tangents along the x-axis.) Hence, the particular solution includes only the semicircle in quadrants III and IV.
Solving x2 + y2 = 25 for y yields The particular solution through point (4,−3) is with domain −5 < x< 5.
Derivatives of Implicitly Defined Functions
In Examples 2 and 3 above, each d.e. was of the form = f (x) or y′ = f (x). We were able to find the general solution in each case very easily by finding the antiderivative
We now consider d.e.’s of the form where f (x,y) is an expression in x and y; that is, is an implicitly defined function. Example 4 illustrates such a differential equation. Here is another example.
EXAMPLE 5
Figure N9–5 shows the slope field for
At each point (x,y) the slope is the sum of its coordinates. Three particular solutions have been added, through the points
FIGURE N9–5
