1. Unit 3 Derivative Rules Of Compositesap Calculus Solver
2. Unit 3 Derivative Rules Of Compositesap Calculus Integrals

Day 3: The Chain Rule (continued) Day 4: Quiz (Topic 3.1) Day 5: Implicit Differentiation. Day 6: Implicit Differentiation (continued) Day 7: Differentiating Inverse Functions. Day 8: Differentiating Inverse Trigonometric Functions. Day 9: Higher-order Derivatives and Derivative Strategies. Day 10: Review Day. Day 11: Unit 3 Test. First Semester (Calculus AP) Syllabus A video tour of the curriculum Calculator doc/video listing Enrichment topics Rev 1 Adobe Flash Player is required to watch the videos. All information regarding Calculus 2-1 and 2-2 class. Unit 3: Derivatives Functions can be analyzed graphically by their limiting behavior and rates of change. At the conclusion of this unit, students will be able to: 1. Evaluate Derivatives 2. Find the equation of a tangent line. 4 weeks Unit 4: Applications of Derivatives. Download Packet: AP Calculus AB / IB Math SL Unit 3: Derivative Rules.

Unit 3 – Derivatives

_________________________________________________________________

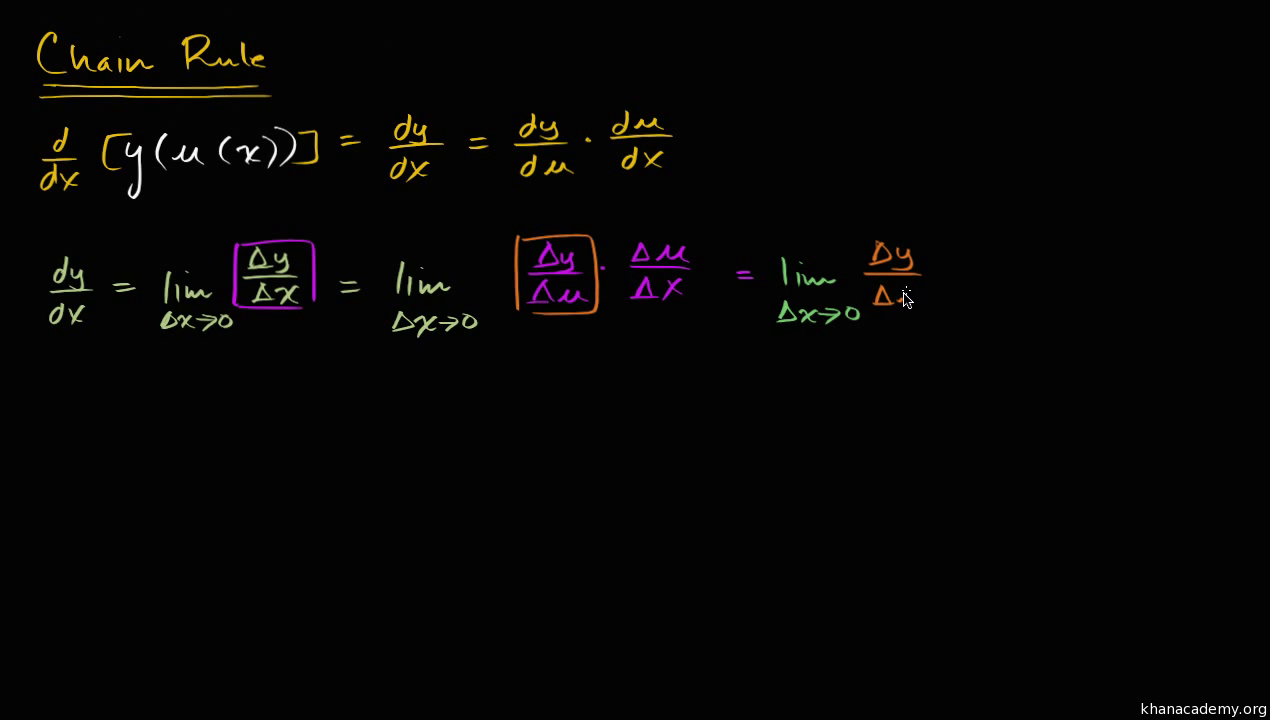
Student Learning Objectives for Unit 3:

Unit 3 Derivative Rules Of Compositesap Calculus Solver

Upon completion of Unit 3, students will be able to

Unit 3 Derivative Rules Of Compositesap Calculus Integrals

• Conceptualize derivative presented graphically, numerically, and analytically.
• Interpret derivative as an instantaneous rate of change
• Calculate slopes and derivatives using the definition of a derivative.
• Graph f from the graph of f’, graph f’ from the graph of f, and graph the derivative of a function given numerically with data.
• Articulate and identify corresponding characteristic of graphs of f and f’
• Determine where a function is not differentiable and distinguish between corners, cusps, discontinuities, and vertical tangents.
• Approximate derivatives from graphs and tables of values
• Know derivatives of basic functions, including power, exponential, logarithmic, trigonometric, and inverse trigonometric functions.
• Use sum, product, quotient, chain rules to calculate derivative of composite functions.
• Use derivative to calculate the instantaneous rate of change.
• Use derivatives to analyze straight line motion and solve other problems involving rates of change.
• Articulate and identify corresponding characteristic of graphs of f, f’, and f”
• Use the graph of f” to identify the points of inflection and concavity of f.
• Use the graph of f’ to identify the local (relative) extrema and the increasing/decreasing behavior of f.
• Find slopes of parameterized curves
• Find derivatives using implicit differentiation.
• Find derivatives using the Power Rule for Rational Powers of x.